Valor de z para un nivel de confianza de 95

1.- Introducción

En estadística, es común hablar de intervalos de confianza, los cuales nos permiten estimar el rango de valores en el cual se encuentra un parámetro poblacional. Para calcular estos intervalos, es necesario conocer el valor de z correspondiente al nivel de confianza deseado. En este artículo, nos enfocaremos en el valor de z para un nivel de confianza de 95.

2.- ¿Qué es z?

z es una variable aleatoria que sigue una distribución normal estándar (con media 0 y desviación estándar 1). Esta distribución es muy útil en estadística, ya que muchas variables aleatorias se pueden aproximar a ella mediante la transformación z = (X - μ) / σ, donde X es la variable original, μ es su media y σ es su desviación estándar.

3.- ¿Para qué sirve el valor de z para un nivel de confianza de 95?

El valor de z para un nivel de confianza de 95 nos indica el número de desviaciones estándar que debemos alejarnos de la media para estar dentro del intervalo de confianza correspondiente. En otras palabras, si queremos construir un intervalo de confianza del 95%, debemos encontrar el valor de z que deja un área del 2.5% en cada cola de la distribución normal estándar (ya que el área central, correspondiente al intervalo de confianza, es del 95%). Este valor de z es aproximadamente 1.96.

4.- ¿Cómo se calcula el valor de z para un nivel de confianza de 95?

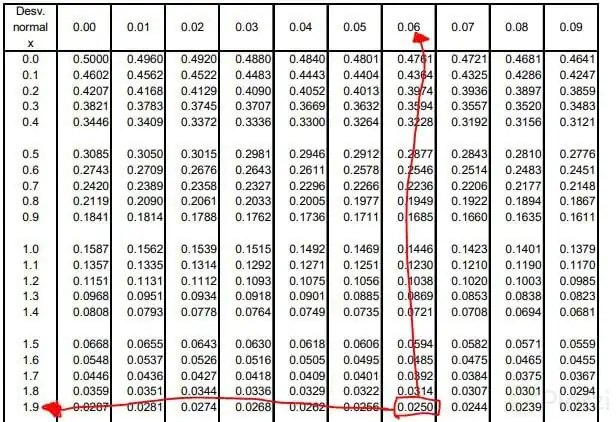
Existen varias formas de obtener el valor de z para un nivel de confianza de 95. Una de ellas es mediante el uso de tablas de distribución normal estándar, las cuales muestran el área acumulada bajo la curva de la distribución para diferentes valores de z. En este caso, debemos buscar el valor de z que deje un área del 0.025 en cada cola de la distribución (ya que queremos un nivel de confianza del 95%). El valor correspondiente es 1.96.

Otra forma de obtener el valor de z es mediante el uso de software estadístico, como R o Python. En estos programas, podemos utilizar la función qnorm(p), donde p es el área acumulada deseada. En el caso de un nivel de confianza del 95%, debemos calcular p = 0.975 (ya que queremos el área que queda a la derecha de -1.96 y a la izquierda de 1.96). El resultado de qnorm(0.975) es también 1.96.

5.- Ejemplo de uso

Supongamos que queremos construir un intervalo de confianza del 95% para la media de una población normal con desviación estándar conocida σ = 2.5 y tamaño muestral n = 100. En este caso, el intervalo estará dado por:

Fórmula del intervalo de confianza
X̄ ± z(α/2) * σ / √n
Donde X̄ es la media muestral, z(α/2) es el valor crítico de z para un nivel de confianza del 95% (es decir, 1.96), σ es la desviación estándar poblacional y n es el tamaño muestral.
Sustituyendo los valores, obtenemos:
X̄ ± 1.96 * 2.5 / √100
Lo cual simplifica a:
X̄ ± 0.49

Esto significa que, con un nivel de confianza del 95%, podemos afirmar que la media poblacional se encuentra en el intervalo (X̄ - 0.49, X̄ + 0.49). Es importante notar que este intervalo depende del tamaño muestral y de la desviación estándar poblacional, por lo que si estos cambian, el intervalo también lo hará.

6.- Conclusión y despedida

El valor de z para un nivel de confianza de 95 nos indica cuántas desviaciones estándar debemos alejarnos de la media para estar dentro del intervalo de confianza correspondiente. Este valor es de aproximadamente 1.96 y se puede obtener mediante tablas de distribución normal estándar o mediante software estadístico. Esperamos que este artículo haya sido útil para comprender mejor este importante concepto en estadística.