Medida de los ángulos agudos de un triángulo rectángulo isósceles

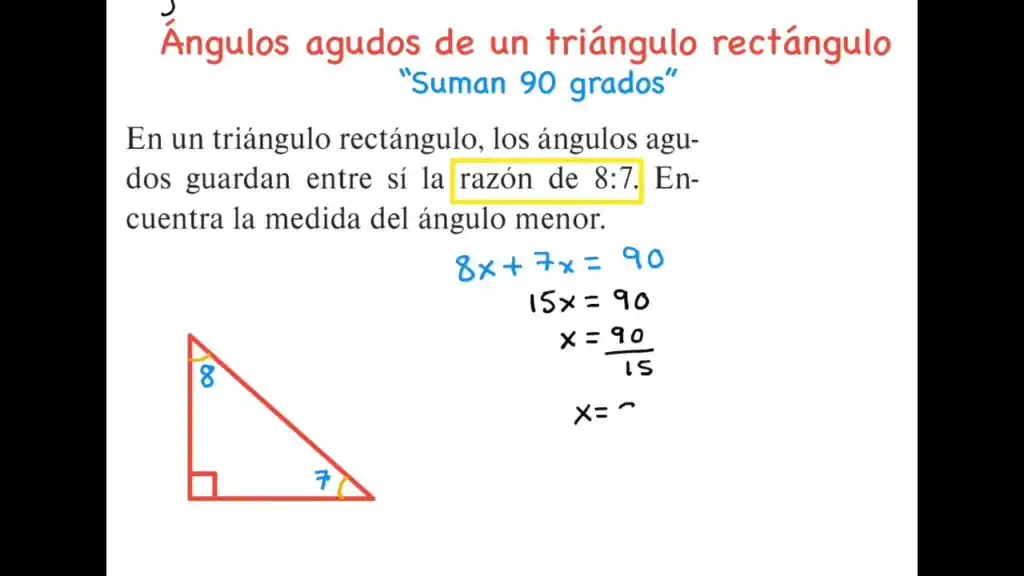
Los triángulos rectángulos son aquellos que tienen un ángulo recto, es decir, un ángulo de 90 grados. Además, en un triángulo rectángulo, los otros dos ángulos agudos suman 90 grados también.

Un triángulo rectángulo isósceles es aquel que tiene dos lados iguales y, por lo tanto, dos ángulos iguales. La medida de los ángulos iguales en un triángulo rectángulo isósceles es de 45 grados cada uno.

Para encontrar la medida de los ángulos agudos restantes en un triángulo rectángulo isósceles, podemos utilizar el teorema de Pitágoras. Este teorema establece que en un triángulo rectángulo, el cuadrado de la hipotenusa (el lado más largo) es igual a la suma de los cuadrados de los otros dos lados.

En un triángulo rectángulo isósceles, los dos lados iguales son los catetos, y la hipotenusa es el lado que falta. Si llamamos a la medida de los catetos "a", la medida de la hipotenusa será "a√2".

Entonces, utilizando el teorema de Pitágoras, podemos encontrar la medida de los ángulos agudos restantes en un triángulo rectángulo isósceles. Primero, elevamos al cuadrado la medida de los catetos y los sumamos:

a² + a² = 2a²

Luego, elevamos al cuadrado la medida de la hipotenusa y la igualamos a la suma de los cuadrados de los catetos:

(a√2)² = 2a²

Desarrollando el cuadrado de la hipotenusa:

2a² = 2a²

Por lo tanto, la medida de los ángulos agudos restantes en un triángulo rectángulo isósceles es de 45 grados cada uno.

Tabla de medidas de ángulos en triángulos rectángulos isósceles

Ángulos	Medida
Ángulos iguales	45 grados cada uno
Ángulo recto	90 grados
Ángulos agudos restantes	45 grados cada uno

La medida de los ángulos agudos de un triángulo rectángulo isósceles es de 45 grados cada uno. Podemos encontrar esta medida utilizando el teorema de Pitágoras y la propiedad de que los ángulos de un triángulo suman 180 grados.