Formula para sacar el area y perimetro de un triangulo

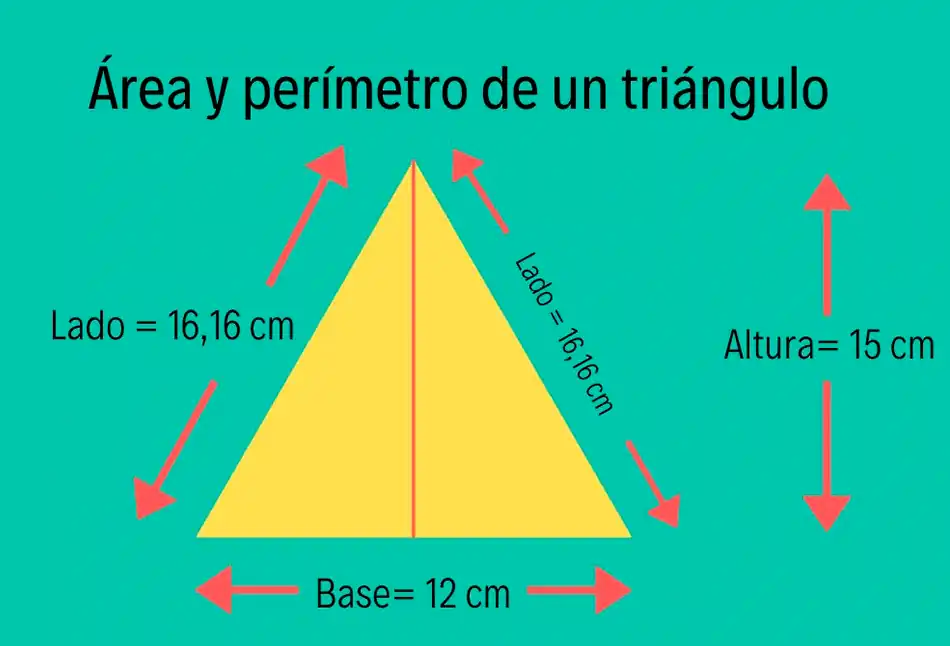
Los triángulos son una de las formas geométricas más simples e importantes en matemáticas. A menudo, necesitamos calcular su área y perímetro para resolver problemas en diferentes campos, como la física, la ingeniería, la arquitectura, entre otros. En este artículo, vamos a aprender cómo calcular el área y perímetro de un triángulo utilizando diferentes fórmulas y técnicas.

Fórmulas básicas

Antes de sumergirnos en las fórmulas específicas para el área y perímetro de un triángulo, es necesario recordar algunas fórmulas básicas que serán útiles. La primera es la fórmula para calcular la longitud de un lado de un triángulo rectángulo utilizando el teorema de Pitágoras:

a² + b² = c²

donde a y b son las longitudes de los catetos y c es la longitud de la hipotenusa.

Otra fórmula importante es la ley de senos, que nos permite calcular la longitud de un lado de un triángulo no rectángulo si conocemos los ángulos y las longitudes de otros dos lados:

a / sen(A) = b / sen(B) = c / sen(C)

Finalmente, la ley de cosenos nos permite calcular la longitud de un lado de un triángulo no rectángulo si conocemos los ángulos y las longitudes de los otros dos lados:

c² = a² + b² - 2ab cos(C)

Cálculo del área de un triángulo

La fórmula básica para calcular el área de un triángulo es:

Área = base x altura / 2

Donde la base es la longitud de uno de los lados del triángulo y la altura es la distancia perpendicular desde la base hasta el vértice opuesto. Si no conocemos la altura, podemos utilizar la fórmula:

Área = 1/2 x b x c x sen(A)

donde b y c son las longitudes de dos lados del triángulo y A es el ángulo opuesto a la base.

Cálculo del perímetro de un triángulo

El perímetro de un triángulo es simplemente la suma de las longitudes de sus tres lados:

Perímetro = a + b + c

Ejemplos de aplicación

Veamos algunos ejemplos de cómo utilizar las fórmulas mencionadas para calcular el área y perímetro de un triángulo:

Ejemplo	Base	Altura	Lado 1	Lado 2	Lado 3	Área	Perímetro
Ejemplo 1	6 cm	4 cm	5 cm	5 cm	6 cm	12 cm²	16 cm
Ejemplo 2	10 cm	8 cm	8 cm	6 cm	10 cm	40 cm²	24 cm
Ejemplo 3	12 cm	9 cm	7 cm	8 cm	10 cm	54 cm²	25 cm

Conclusiones y despedida

Como hemos visto, el cálculo del área y perímetro de un triángulo puede ser muy útil en diferentes campos. Aunque existen diferentes fórmulas y técnicas para hacerlo, lo más importante es comprender los conceptos básicos y aplicarlos de manera adecuada. Esperamos que este artículo haya sido de utilidad y te invitamos a seguir aprendiendo sobre geometría y matemáticas en general.