Expresión analítica de una función a partir de su gráfica

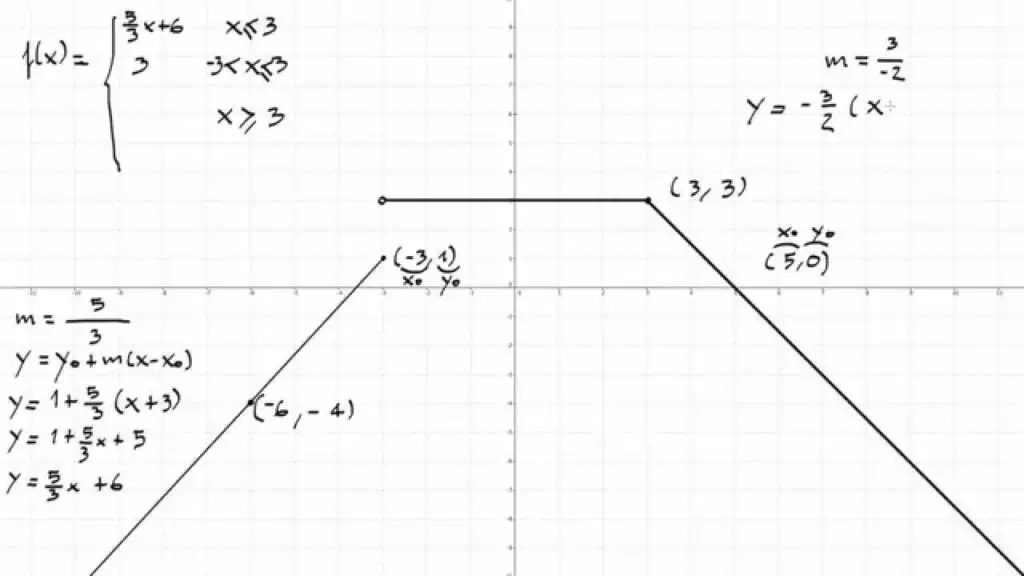
La expresión analítica de una función es una herramienta fundamental en el campo de las matemáticas. Esta permite conocer con exactitud el comportamiento de una función en cualquier punto del dominio. Sin embargo, en algunos casos, obtener la expresión analítica de una función puede resultar complicado. En este artículo, te explicaremos cómo obtener la expresión analítica de una función a partir de su gráfica.

Antes de comenzar, es importante tener en cuenta que no todas las funciones pueden ser descritas por una expresión analítica. Algunas funciones son tan complejas que no existe una fórmula matemática que las describa de manera exacta. Sin embargo, en la mayoría de los casos, es posible obtener una aproximación bastante cercana utilizando métodos gráficos.

Identificación de puntos importantes

El primer paso para obtener la expresión analítica de una función a partir de su gráfica es identificar los puntos importantes que aparecen en ella. Estos puntos pueden ser los extremos (máximos y mínimos), los puntos de inflexión, los interceptos con los ejes, entre otros.

Una vez identificados los puntos importantes, podemos comenzar a buscar patrones o regularidades que nos ayuden a deducir la expresión analítica de la función. Por ejemplo, si la gráfica de la función es una recta, podemos utilizar la ecuación de la recta para obtener su expresión analítica.

Aproximación mediante polinomios

En algunos casos, es posible aproximar la función por medio de un polinomio. Para hacer esto, podemos utilizar el método de interpolación de Lagrange, que nos permite encontrar un polinomio que pase por un conjunto dado de puntos en la gráfica.

Una vez obtenido el polinomio, podemos utilizarlo como una aproximación de la función original. Esta aproximación será más precisa cuanto mayor sea el grado del polinomio utilizado.

Aproximación mediante series de Taylor

Otro método para obtener la expresión analítica de una función a partir de su gráfica es mediante el uso de series de Taylor. Este método consiste en aproximar la función por medio de una serie de polinomios cuyos coeficientes están relacionados con las derivadas de la función en un punto dado.

Al igual que en el método de interpolación de Lagrange, la aproximación obtenida mediante series de Taylor será más precisa cuanto mayor sea el número de términos de la serie utilizado.

Ejemplo práctico

Para ilustrar lo explicado anteriormente, consideremos la gráfica de la siguiente función:

x	0	1	2	3	4
y	0	1	4	9	16

En este caso, podemos observar que la gráfica de la función es una parábola que pasa por los puntos (0,0), (1,1), (2,4), (3,9) y (4,16). Utilizando el método de interpolación de Lagrange, podemos obtener un polinomio de segundo grado que pase por estos puntos:

y = x²

Como se puede observar, este polinomio es una aproximación bastante cercana de la función original y nos permite obtener su expresión analítica de manera sencilla.

Conclusión y despedida

Obtener la expresión analítica de una función a partir de su gráfica puede resultar un proceso complicado en algunos casos. Sin embargo, existen varios métodos que nos permiten aproximar la función de manera precisa utilizando únicamente la información proporcionada por su gráfica.

Esperamos que este artículo te haya sido útil y que puedas aplicar estos métodos en tus futuros estudios de matemáticas.