Ejemplos de como sacar el area de un triangulo isosceles

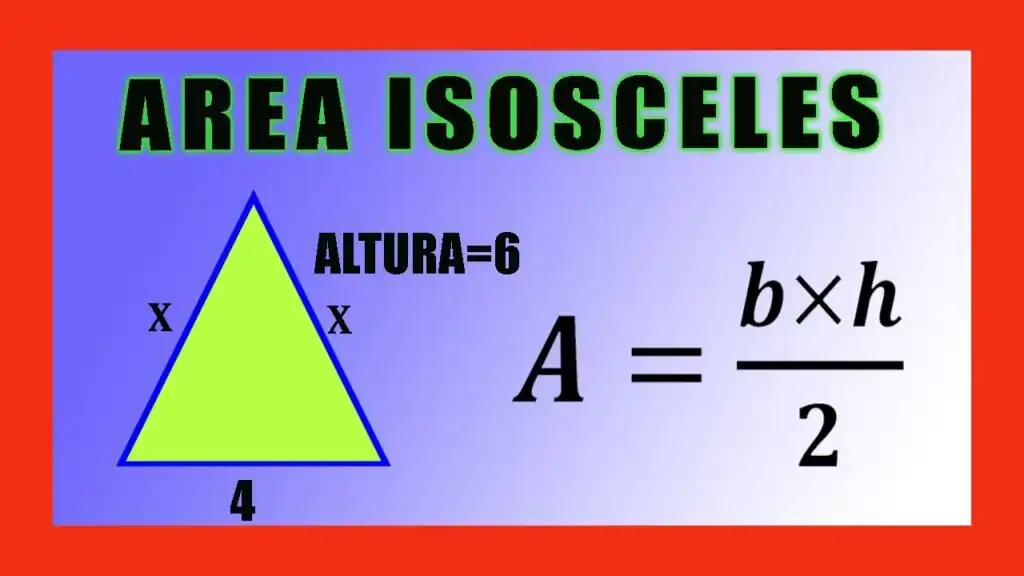
Los triángulos isósceles son aquellos que tienen dos lados iguales y un ángulo opuesto a esos lados también igual. El cálculo del área de un triángulo isósceles es un tema importante en la geometría, y existen diferentes maneras de hacerlo. En este artículo, presentamos algunos ejemplos de cómo sacar el área de un triángulo isósceles.

Fórmula básica

Una forma sencilla de calcular el área de un triángulo isósceles es utilizando la fórmula básica:

Ejemplos de como sacar el area de un triangulo isosceles:

Área = (base x altura) / 2

Donde la base es uno de los lados iguales y la altura es la distancia desde la base hasta el vértice opuesto. Veamos un ejemplo:

Lado igual	Base	Altura	Área
5 cm	8 cm	4.5 cm	18 cm²

En este ejemplo, la base del triángulo es de 8 cm y la altura es de 4.5 cm. Entonces, el área del triangulo isósceles es de 18 cm².

Teorema de Pitágoras

Otra manera de calcular el área de un triángulo isósceles es utilizando el teorema de Pitágoras. Este teorema establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. En el caso de un triángulo isósceles, la altura se convierte en la bisectriz del ángulo opuesto a la base, y al dividir el triángulo en dos triángulos rectángulos, podemos aplicar el teorema de Pitágoras.

Ejemplos de como sacar el area de un triangulo isosceles:

Área = (base x altura) / 2

Altura = sqrt(lado igual² - (base/2)²)

Veamos un ejemplo:

Lado igual	Base	Altura	Área
10 cm	6 cm	8.66 cm	26 cm²

En este ejemplo, la base del triángulo es de 6 cm y la altura es de 8.66 cm (calculada utilizando el teorema de Pitágoras). Entonces, el área del triangulo isósceles es de 26 cm².

Fórmula de Herón

La fórmula de Herón es una fórmula general para calcular el área de cualquier triángulo, no solo los isósceles. Esta fórmula se basa en el semiperímetro del triángulo, que es la mitad de la suma de sus tres lados.

Ejemplos de como sacar el area de un triangulo isosceles:

Área = sqrt(s(s-a)(s-b)(s-b))

Donde s = (a+b+c)/2

Veamos un ejemplo:

Lado igual	Base	Área
6 cm	8 cm	14.42 cm²

En este ejemplo, la base del triángulo es de 8 cm y el lado igual es de 6 cm (calculado como la mitad de la base). Entonces, el área del triangulo isósceles es de 14.42 cm².

Conclusión y despedida

En este artículo hemos visto diferentes maneras de calcular el área de un triángulo isósceles. Dependiendo de la información que tengamos sobre el triángulo (base, altura o lados iguales), podemos utilizar una u otra fórmula para obtener el resultado deseado.

Esperamos que estos ejemplos de como sacar el area de un triangulo isosceles te hayan sido de ayuda y te permitan resolver problemas relacionados con la geometría de los triángulos.